Master's and Bachelor's Project and Thesis Proposals

I primarily work in in spatial and spatiotemporal methods and their applications, among other things, and have a number of potential projects and thesis topics for interested Master's and Bachelor's students. Some of these topics are shown in detail below. Please contact me if you are interested in these, or if you have other topics you are interested in studying together. Depending on whether you are a Master's or Bachelor's student, topics can be adjusted to your background.

Inferring Historical Magnitude 9 Earthquake Coseismic Slip Distributions Using Paleoseismic Evidence (Continuation)

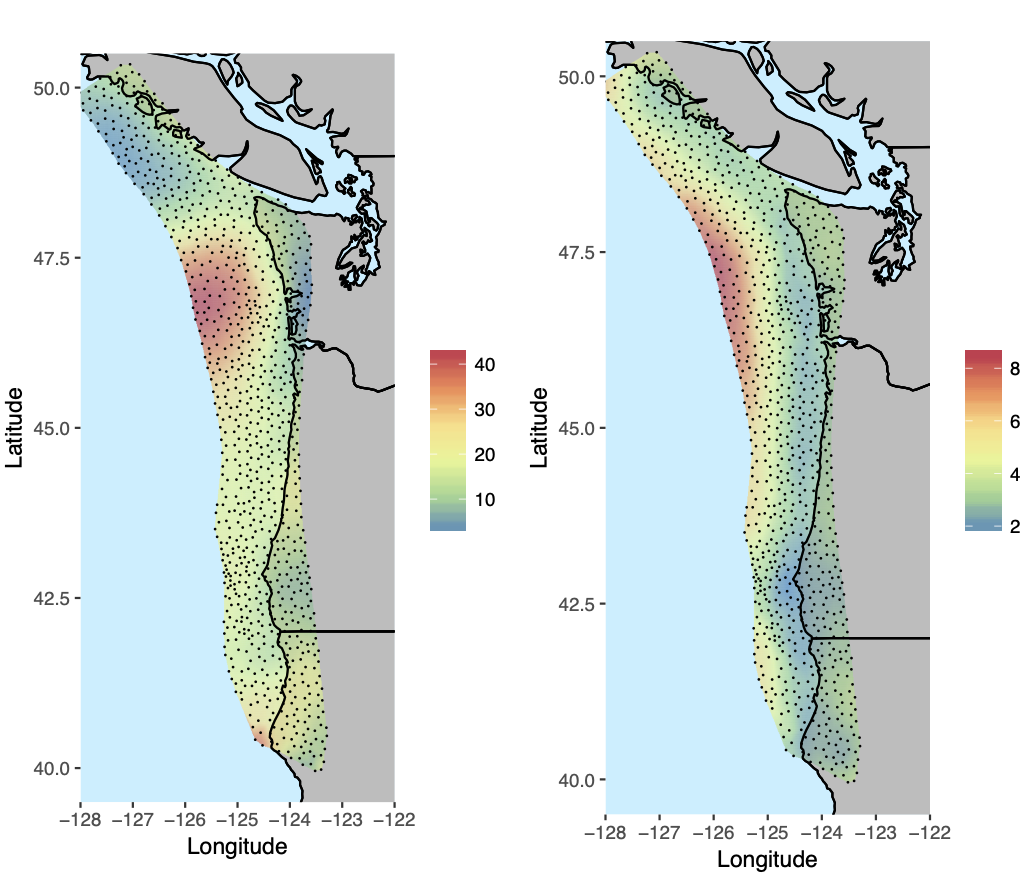
The Cascadia Subduction Zone (CSZ) is a 1,000 km long fault off the west coast of North America stretching from northern California in the US to Vancouver Island, Canada. The CSZ is capable of producing magnitude 9 earthquakes, but it has not experienced one since 1700. Historic evidence is therefore necessary to be able to assess risk due to future earthquakes. One such source of evidence is estimates of paleoseismic subsidence along the coast, where carbon dated measurements of how much the ground sank as a result of past earthquakes can be used to infer how large the associated earthquakes were, and where along the coast risk from future earthquakes is highest.

This project will involve continuing work from a previous Master's thesis, and potentially collaborations with Seismologists and other Statisticians. It will certainly involve “inverse modeling” of earthquake spatial slip distributions using a combination of 1) existing Python code from R for a “forward model” that predicts subsidence given an input earthquake, and 2) a spatial model for CSZ earthquakes. The forward model is linked to the statistical earthquake model to assess the size and spatial distribution of past and future earthquakes, which could result in a paper in a peer reviewed journal depending on progress.

A strong statistical background is required, along with strong programming experience in R and ideally some programming experience in Python as well. Some understanding of spatial statistics would be ideal, but not necessary.

Cross Validation in a Spatial Context

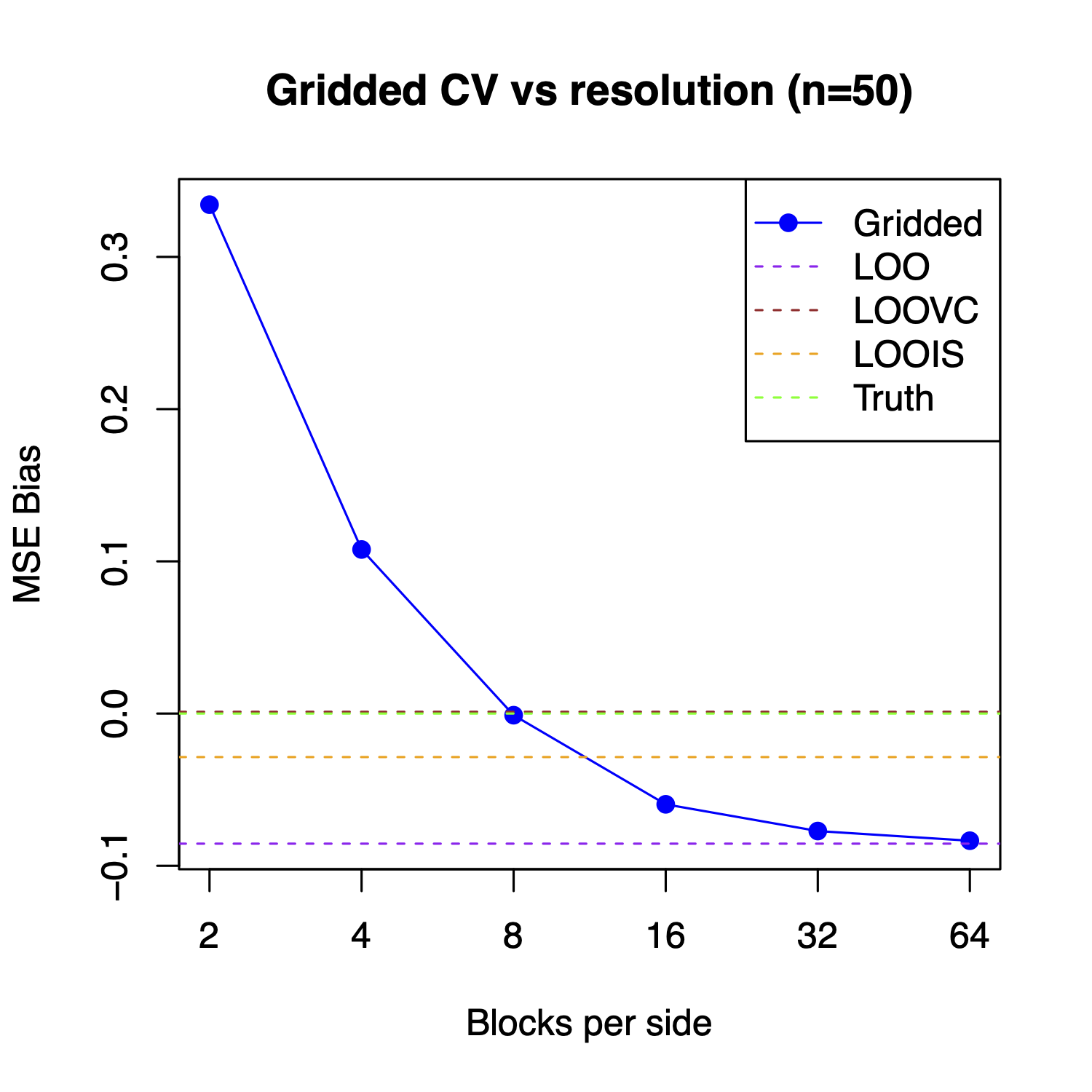
How does one decide what models are better than others? Classically, one may use leave one out cross validation (LOOCV), leaving out one observation at a time and calculating the squared error of the prediction. The average of these errors over each observation can then be used to estimate a model's average predictive error, and the model with the smallest predictive error is then considered the best. However, this form of validation ignores spatial correlation in observation locations and in predictions, and often leads to biased estimates of predictive error in the context of spatial datasets, potentially even leading to poor choices of models.

This project will involve exploring when LOOCV, among other traditional methods for validation such as blocked/gridded cross validation, perform poorly in terms of both bias and MSE in the predictive error estimate, and in terms of model selection. Depending on progress, this project could expand into an exploration of methods that may work well in contexts where LOOCV and block cross validation may fail. In addition, it may result in a publication in a peer-reviewed journal.

A strong statistical background is required, along with strong programming experience in R. Some understanding of spatial statistics and/or survey statistics would be ideal, but not necessary.

Accounting for Positional Error in Spatial Models: Local Adaptation of Numerical Integration

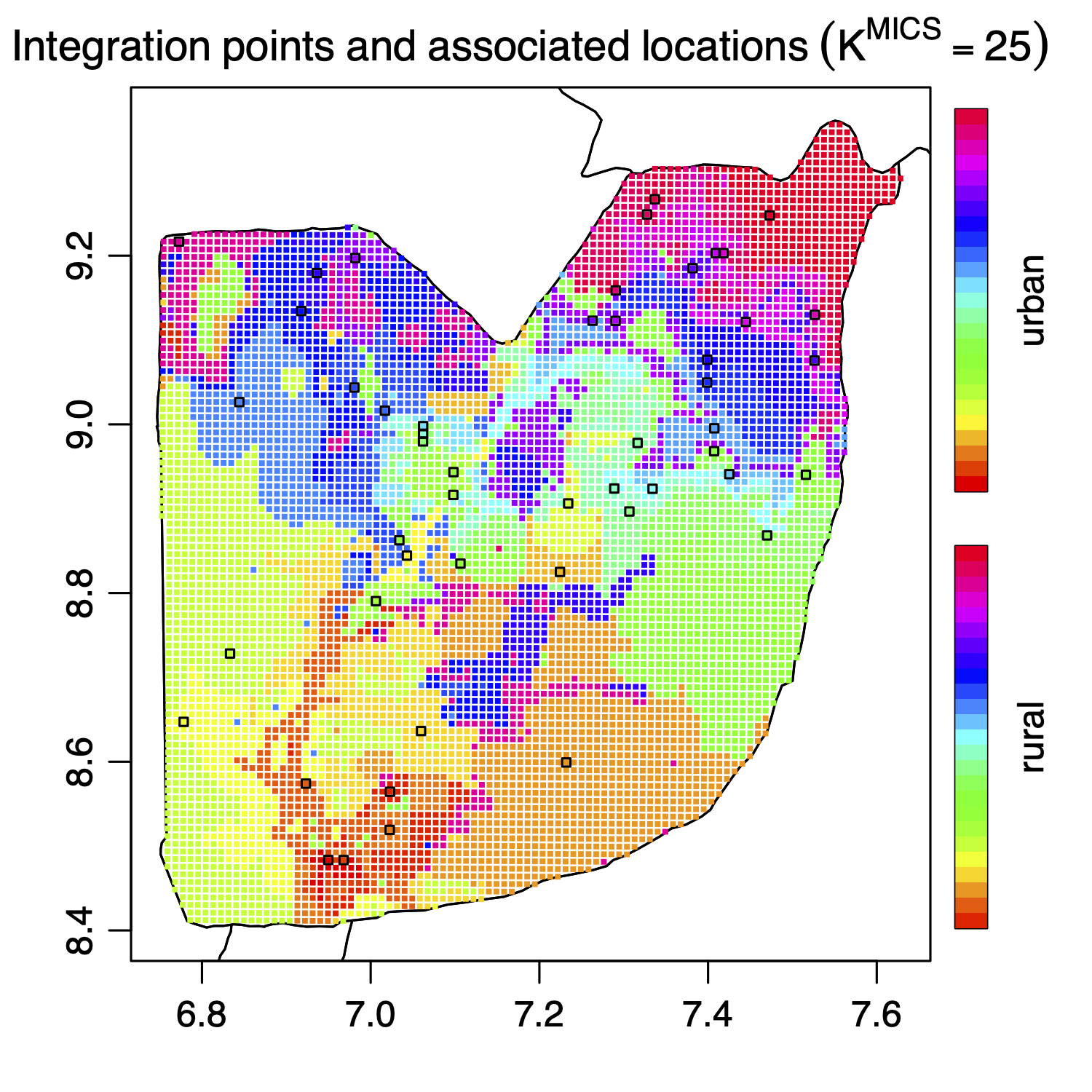
Spatial models are statistical models that account for the fact that nearby observations tend to be more similar (i.e. correlated) than ones that are far away. As the distance between observations increases, spatial models explicitely model how their correlation is accordingly reduced.

Traditional spatial models assume that the spatial point location of each observation is known exactly. However, the location may be unknown, such as when the location is deliberately censored or randomly adjusted for confidentiality purposes. This induces uncertainty in the spatial location (called 'positional' or 'locational' uncertianty), and may affect predictions. One technique for accounting for such uncertainty involves numerical integration of the likelihood over possible positions of the true location over a number of integration points. However, this technique could be improved by adapting the integration scheme for each observation, choosing a minimal number of integration points while maintaining accurate estimates.

The student would be responsible for updating code for the statistical model by allowing for a variable number of integration points for each observation, and evaluating the performance of a numerical integral via prespecified evaluation criteria. Depending on progress, this project may result in a publication in a peer-reviewed journal, or in your contribution to a publically available repository on CRAN.

A strong background in programming in R is required along with a strong statistical background in statistics. Some understanding of spatial statistics and C++ would be ideal, but not necessary.

Other Topics

The above thesis and project topics are not all-inclusive. If you have a topic you are particularly interested in, you are welcome to ask me if I would be willing to supervise it. In addition, there are other ideas I have for topics related to making an R package for constructing multivariate simplex splines, creating proper scoring rules for discrete outcomes, Bayesian model averaging, penalized survey/design-based regression estimators, multivariate priors for spatial models, Bayesian neural estimators, Bayesian deep GMRFs, and potentially more. Again, if you are interested in studying any of these topics, those listed above, or others, please contact me.